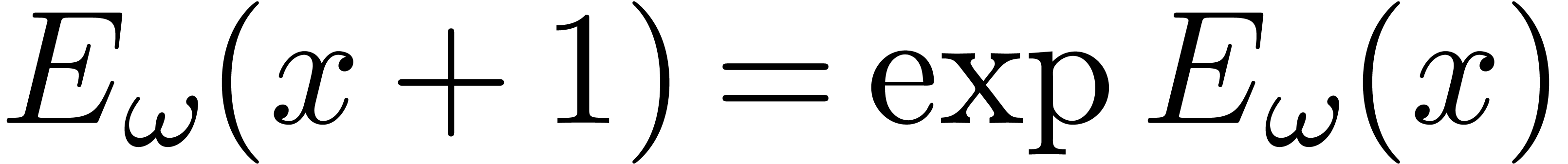may have solutions that grow faster than any iterated exponential and
thereby faster than any transseries.
| HomepagePublicationsTalksTeXmacsMathemagix |
Transseries provide a universal framework for the formal asymptotics of
regular solutions to ordinary differential equations at infinity. More
general functional equations such as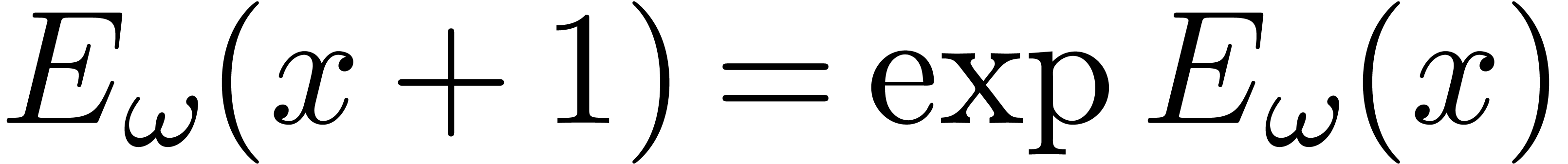
may have solutions that grow faster than any iterated exponential and
thereby faster than any transseries.
In order to develop a truly universal framework for the asymptotics of
regular univariate functions at infinity, we therefore need a
generalization of transseries: hyperseries. Hyperexponentials and
hyperlogarithms play a central role in such a program. The first
non-trivial hyperexponential and hyperlogarithm are 
and its functional inverse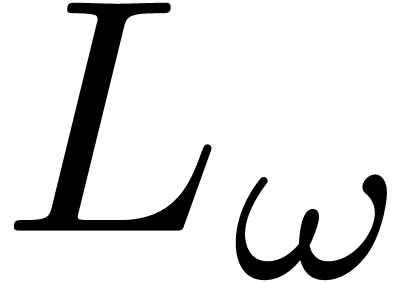 
, where
satisfies the above equation. Formally, such functions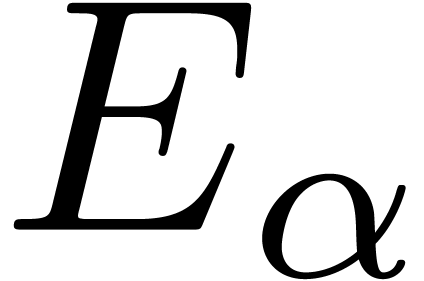 
and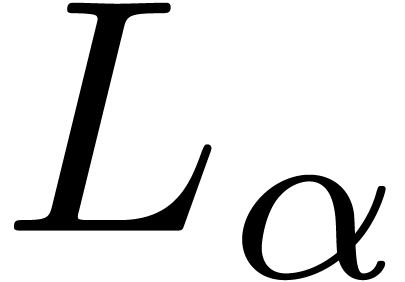 
can be introduced for any ordinal 
.
For instance,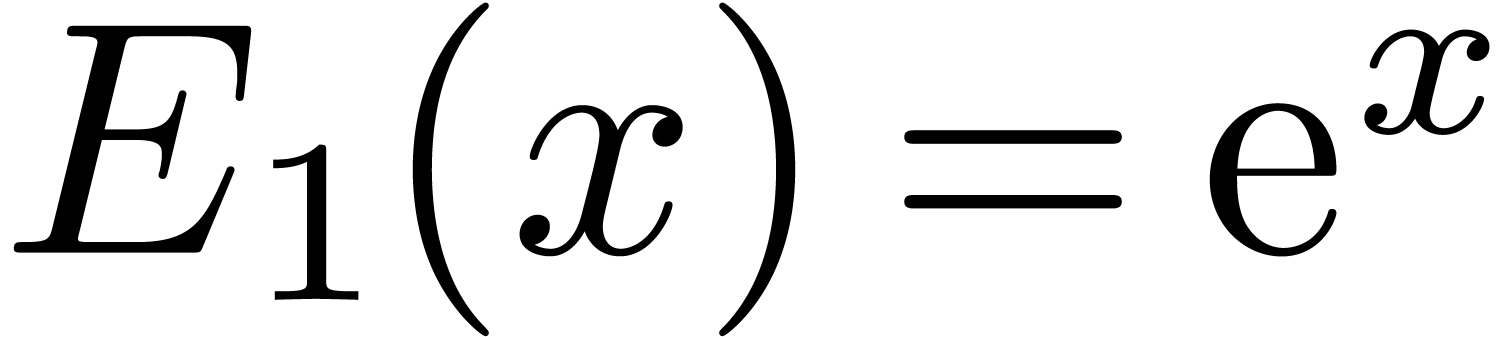 
, 
, 
,
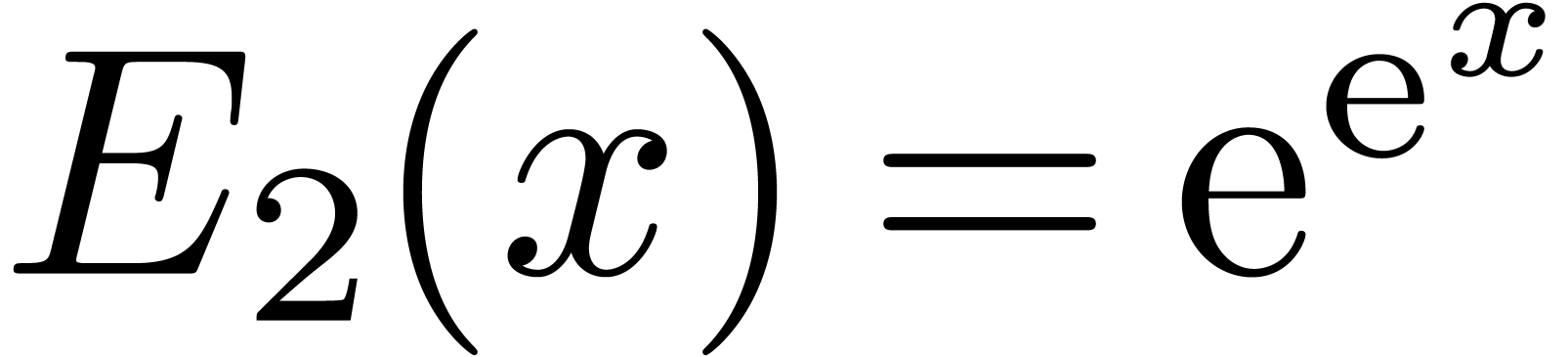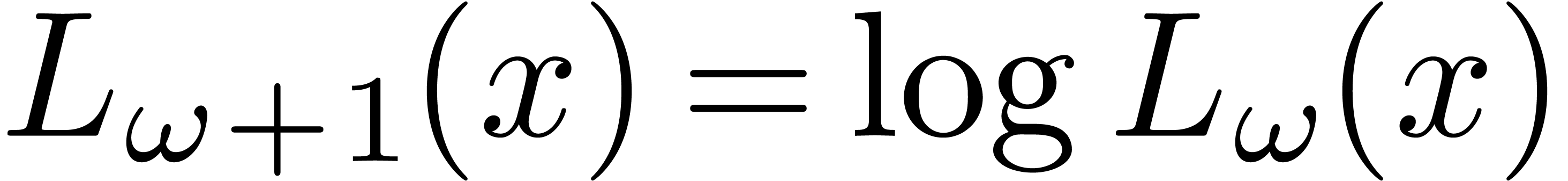and 
satisfies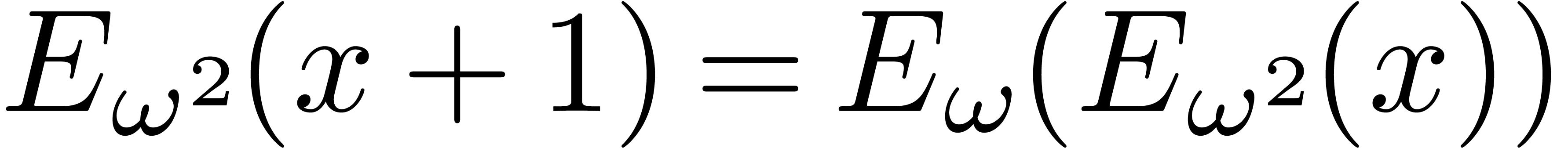 
.
In the present work, we construct a field of hyperseries that is closed
under 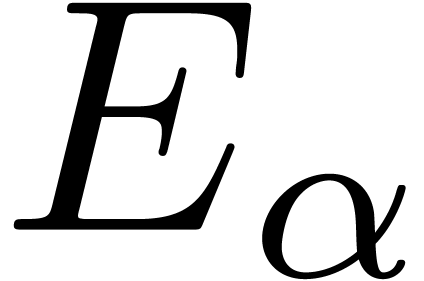and 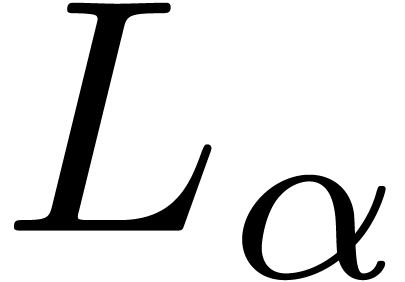for all ordinals .
This generalizes previous work by Schmeling in the case
when 
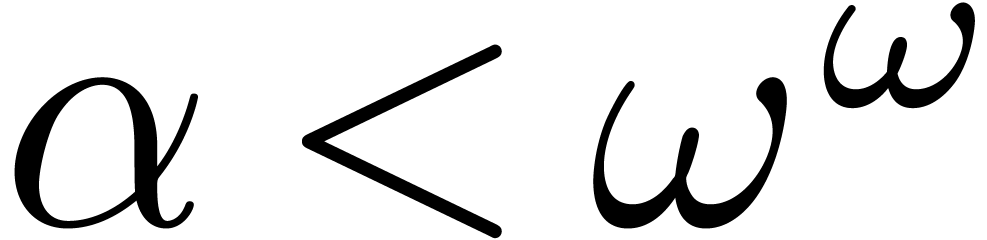, as well as the previous construction of the field of logarithmic hyperseries
by van den Dries, van der Hoeven, and Kaplan.
Authors:
Keywords: hyperseries, transseries, asymptotic analysis, growth scale, surreal number