Abstract
The best known asymptotic bit complexity bound for factoring univariate
polynomials over finite fields grows with the input degree to a power
close to 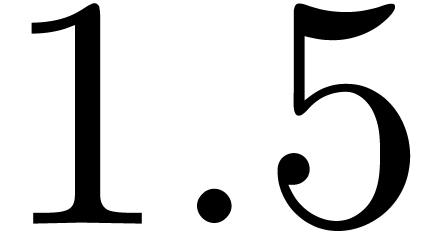 , and with the
square of the bitsize of the ground field. It relies on a variant of the
Cantor–Zassenhaus algorithm which exploits fast modular
composition. Using techniques by Kaltofen and Shoup, we prove a
refinement of this bound when the finite field has a large extension
degree over its prime field. We also present fast practical algorithms
for the case when the extension degree is smooth.
, and with the
square of the bitsize of the ground field. It relies on a variant of the
Cantor–Zassenhaus algorithm which exploits fast modular
composition. Using techniques by Kaltofen and Shoup, we prove a
refinement of this bound when the finite field has a large extension
degree over its prime field. We also present fast practical algorithms
for the case when the extension degree is smooth.
Authors: Joris van der Hoeven,
Grégoire Lecerf
View: Html, TeXmacs, Pdf,
BibTeX
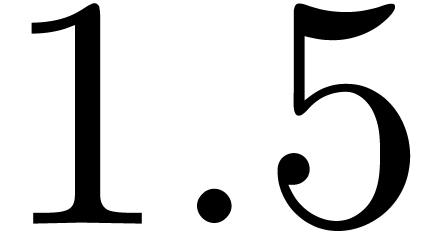 , and with the
square of the bitsize of the ground field. It relies on a variant of the
Cantor–Zassenhaus algorithm which exploits fast modular
composition. Using techniques by Kaltofen and Shoup, we prove a
refinement of this bound when the finite field has a large extension
degree over its prime field. We also present fast practical algorithms
for the case when the extension degree is smooth.
, and with the
square of the bitsize of the ground field. It relies on a variant of the
Cantor–Zassenhaus algorithm which exploits fast modular
composition. Using techniques by Kaltofen and Shoup, we prove a
refinement of this bound when the finite field has a large extension
degree over its prime field. We also present fast practical algorithms
for the case when the extension degree is smooth.