Abstract
It is well known that Hardy fields can be extended with integrals,
exponentials and solutions to Pfaffian first order differential
equations 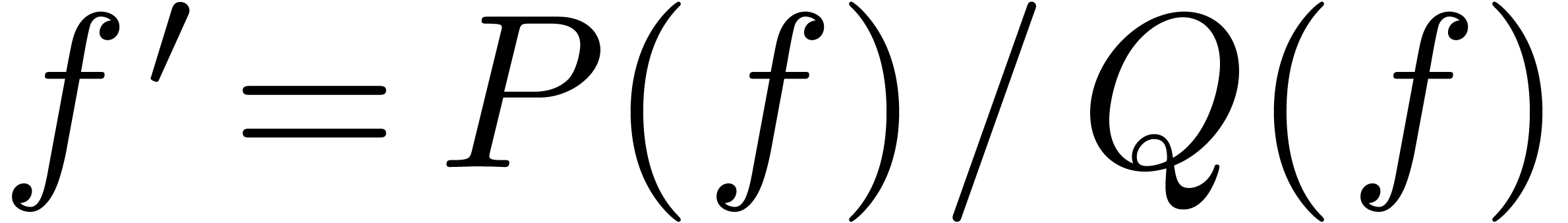 . From the formal
point of view, the theory of transseries allows for the resolution of
more general algebraic differential equations. However, until now, this
theory did not admit a satisfactory analytic counterpart. In this paper,
we will introduce the notion of a transserial Hardy field. Such fields
combine the advantages of Hardy fields and transseries. In particular,
we will prove that the field of differentially algebraic transseries
over
. From the formal
point of view, the theory of transseries allows for the resolution of
more general algebraic differential equations. However, until now, this
theory did not admit a satisfactory analytic counterpart. In this paper,
we will introduce the notion of a transserial Hardy field. Such fields
combine the advantages of Hardy fields and transseries. In particular,
we will prove that the field of differentially algebraic transseries
over 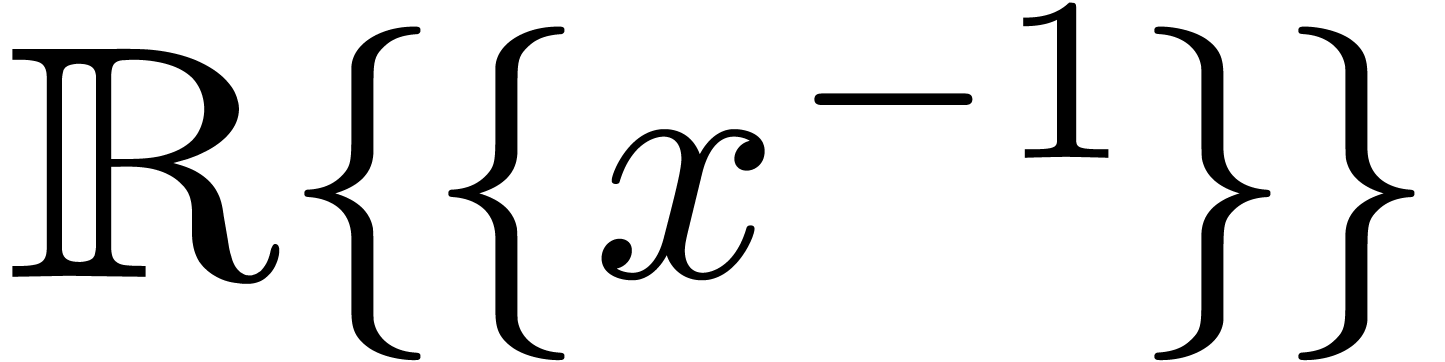 carries a transserial
Hardy field structure. Inversely, we will give a sufficient condition
for the existence of a transserial Hardy field structure on a given
Hardy field.
carries a transserial
Hardy field structure. Inversely, we will give a sufficient condition
for the existence of a transserial Hardy field structure on a given
Hardy field.
Keywords: transseries, Hardy field, o-minimality,
algebraic differential equation
A.M.S. subject classification: 26A12, 34E05, 40A05,
03C64
View: Html, TeXmacs, Pdf,
BibTeX
Revised version (2017, February, 7): Pdf
Acknowledgment: Lou van den
Dries and Mickaël Matusinski kindly
provided me with feedback that has given rise to the revised version
with various corrections and improvements concerning the readability.
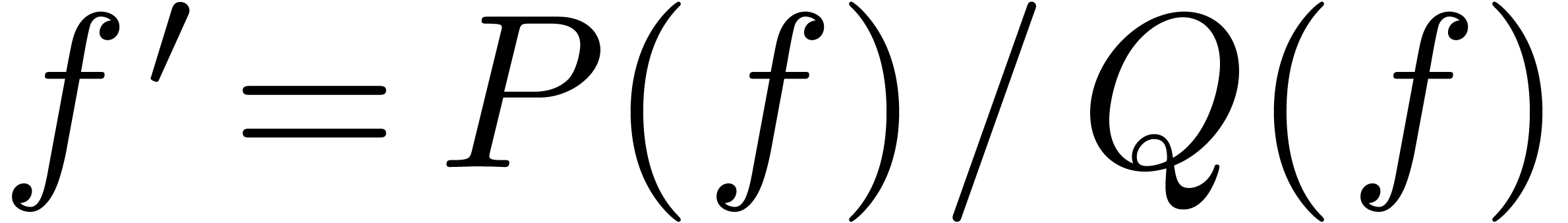 . From the formal
point of view, the theory of transseries allows for the resolution of
more general algebraic differential equations. However, until now, this
theory did not admit a satisfactory analytic counterpart. In this paper,
we will introduce the notion of a transserial Hardy field. Such fields
combine the advantages of Hardy fields and transseries. In particular,
we will prove that the field of differentially algebraic transseries
over
. From the formal
point of view, the theory of transseries allows for the resolution of
more general algebraic differential equations. However, until now, this
theory did not admit a satisfactory analytic counterpart. In this paper,
we will introduce the notion of a transserial Hardy field. Such fields
combine the advantages of Hardy fields and transseries. In particular,
we will prove that the field of differentially algebraic transseries
over 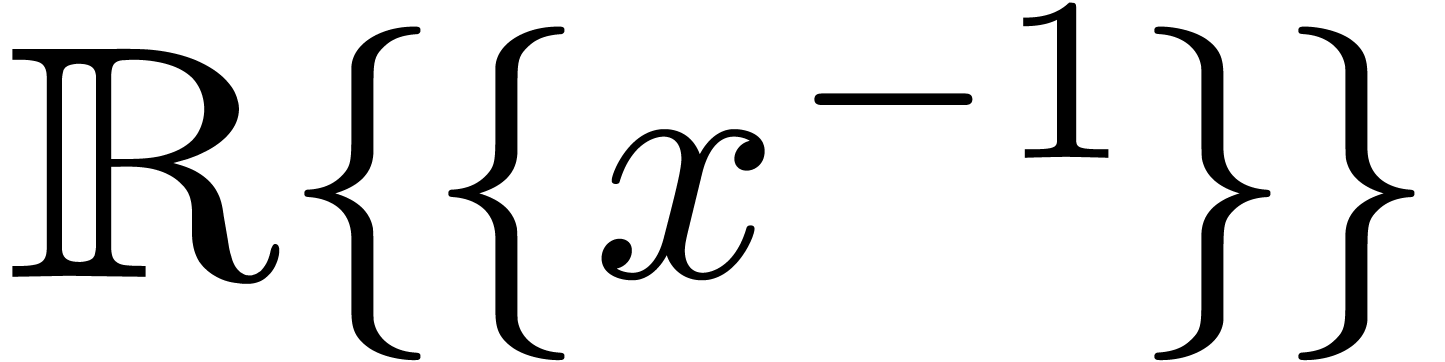 carries a transserial
Hardy field structure. Inversely, we will give a sufficient condition
for the existence of a transserial Hardy field structure on a given
Hardy field.
carries a transserial
Hardy field structure. Inversely, we will give a sufficient condition
for the existence of a transserial Hardy field structure on a given
Hardy field.