 the field of transseries,
the intermediate value theorem states that for any differential
polynomials
the field of transseries,
the intermediate value theorem states that for any differential
polynomials 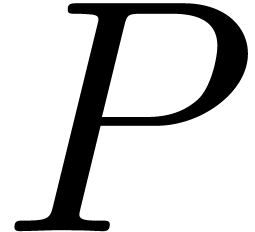 with
coefficients in
with
coefficients in  and
and 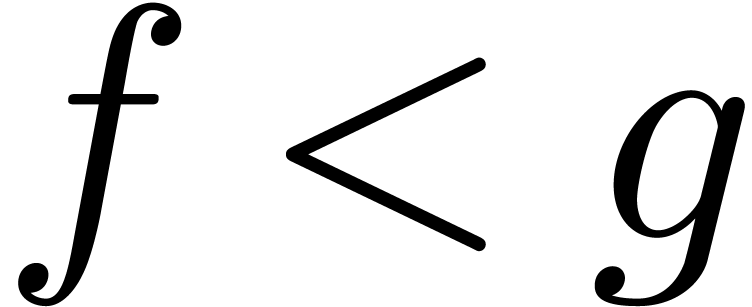 in
in  with
with 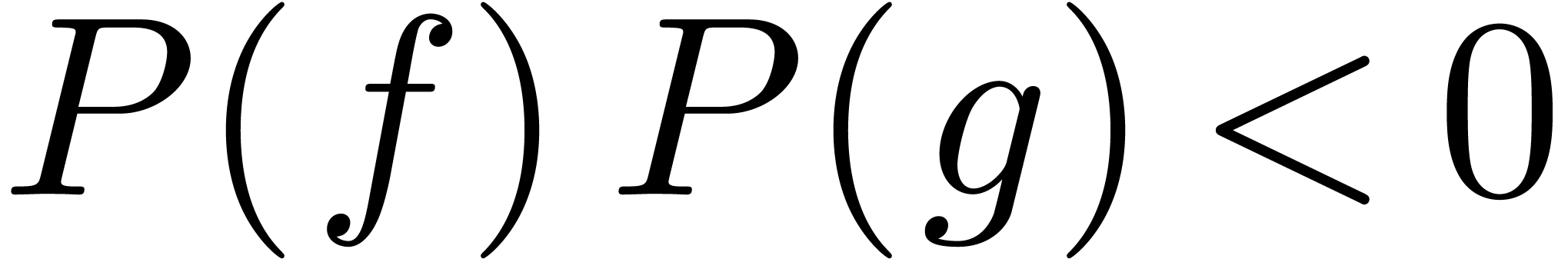 , there exists a
solution
, there exists a
solution 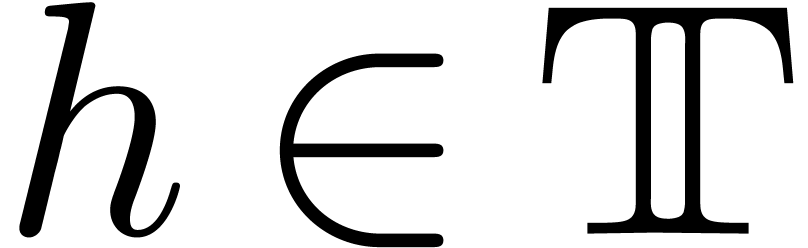 to
to 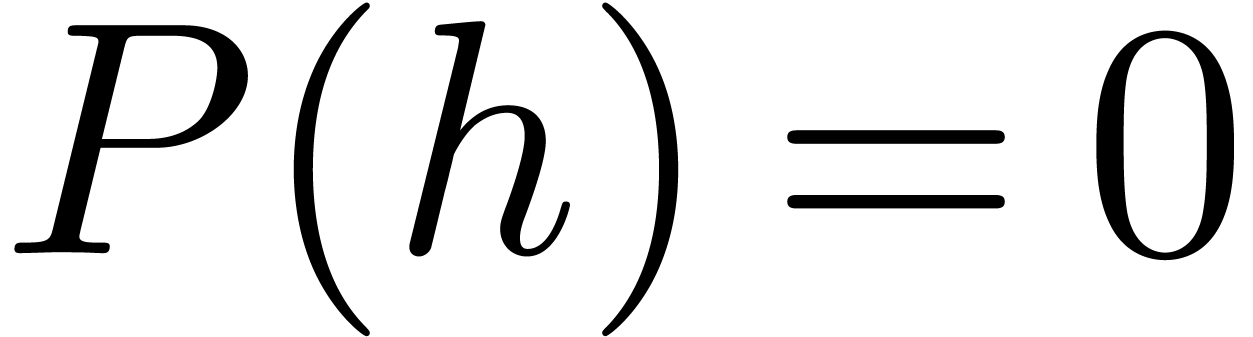 with
with 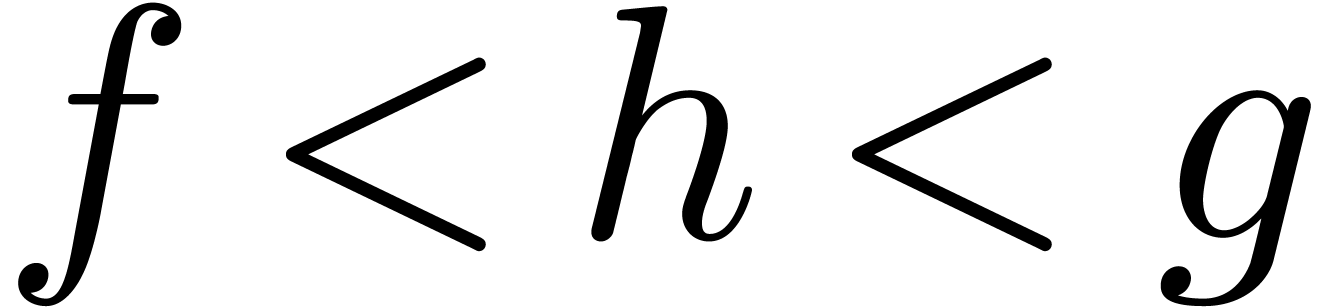 .
.
| HomepagePublicationsTalksTeXmacsMathemagix |
In this survey paper, we outline the proof of a recent differential
intermediate value theorem for transseries. Transseries are a
generalization of power series with real coefficients, in which one
allows the recursive appearance of exponentials and logarithms. Denoting
by  the field of transseries,
the intermediate value theorem states that for any differential
polynomials
the field of transseries,
the intermediate value theorem states that for any differential
polynomials  with
coefficients in
with
coefficients in  and
and  in
in  with
with 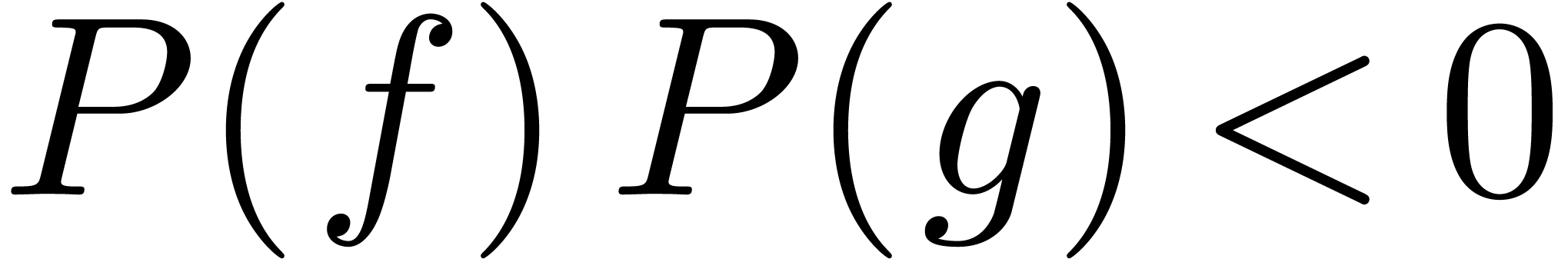 , there exists a
solution
, there exists a
solution 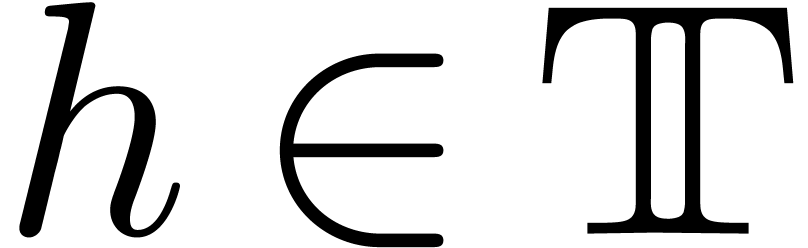 to
to 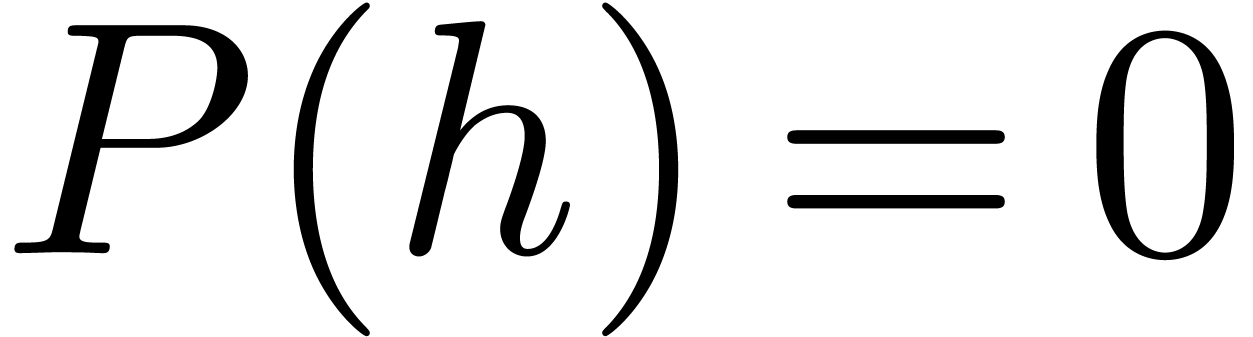 with
with 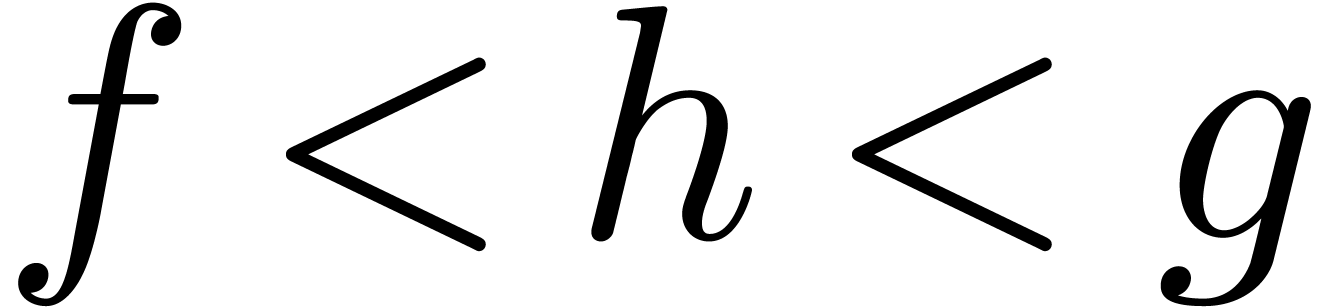 .
.
View: Html, TeXmacs, Pdf, BibTeX
See also: the corresponding preprint with details