Abstract
We give a new proof of Fürer's bound for the cost of multiplying
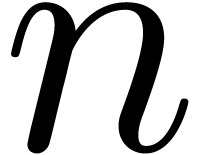 -bit integers in the bit
complexity model. Unlike Fürer, our method does not require
constructing special coefficient rings with “fast” roots of
unity. Moreover, we prove the more explicit bound
-bit integers in the bit
complexity model. Unlike Fürer, our method does not require
constructing special coefficient rings with “fast” roots of
unity. Moreover, we prove the more explicit bound 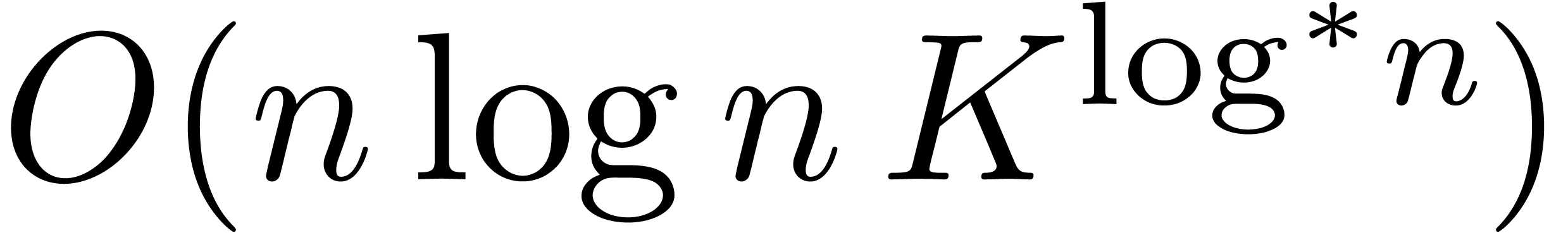 with
with 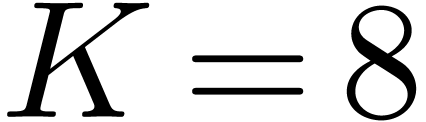 .
We show that an optimised variant of Fürer's algorithm achieves
only
.
We show that an optimised variant of Fürer's algorithm achieves
only 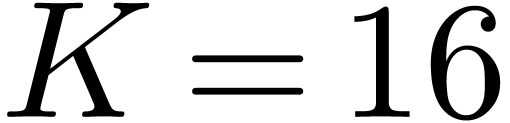 , suggesting that the
new algorithm is faster than Fürer's by a factor of
, suggesting that the
new algorithm is faster than Fürer's by a factor of 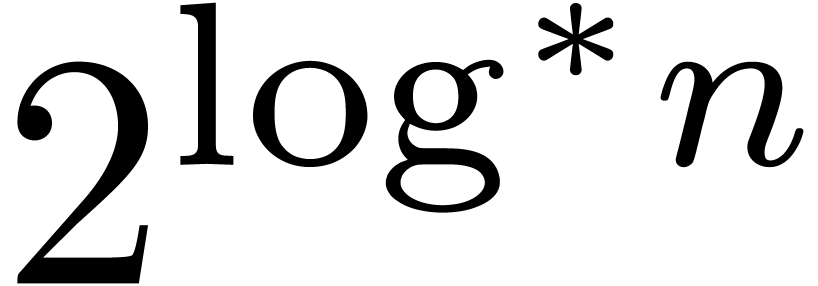 . Assuming standard conjectures about the
distribution of Mersenne primes, we give yet another algorithm that
achieves
. Assuming standard conjectures about the
distribution of Mersenne primes, we give yet another algorithm that
achieves 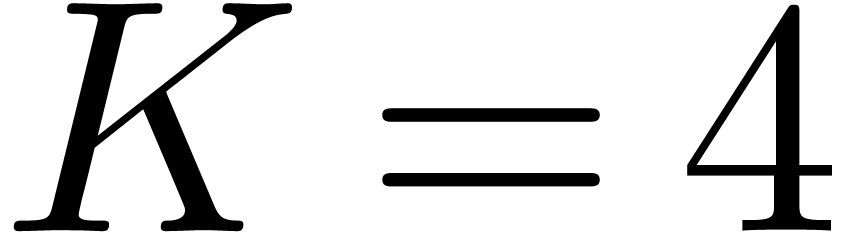 .
.
Authors: David Harvey, Joris van der Hoeven, Grégoire
Lecerf
Keywords: Integer multiplication, algorithm, complexity
bound, FFT
A.M.S. subject classification: 68W30, 68Q17, 68W40
View: Html, TeXmacs, Pdf,
BibTeX
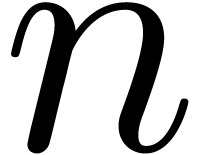 -bit integers in the bit
complexity model. Unlike Fürer, our method does not require
constructing special coefficient rings with “fast” roots of
unity. Moreover, we prove the more explicit bound
-bit integers in the bit
complexity model. Unlike Fürer, our method does not require
constructing special coefficient rings with “fast” roots of
unity. Moreover, we prove the more explicit bound 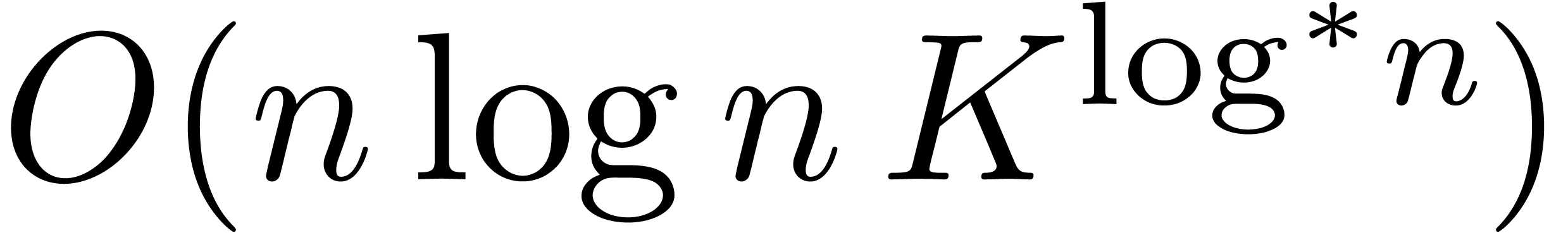 with
with 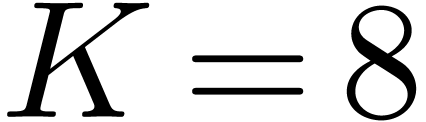 .
We show that an optimised variant of Fürer's algorithm achieves
only
.
We show that an optimised variant of Fürer's algorithm achieves
only 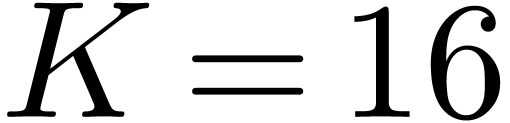 , suggesting that the
new algorithm is faster than Fürer's by a factor of
, suggesting that the
new algorithm is faster than Fürer's by a factor of 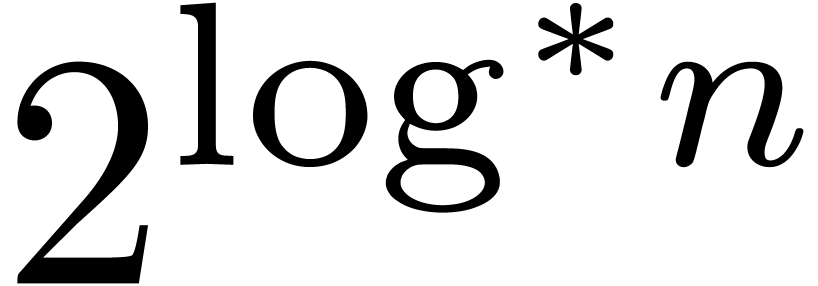 . Assuming standard conjectures about the
distribution of Mersenne primes, we give yet another algorithm that
achieves
. Assuming standard conjectures about the
distribution of Mersenne primes, we give yet another algorithm that
achieves 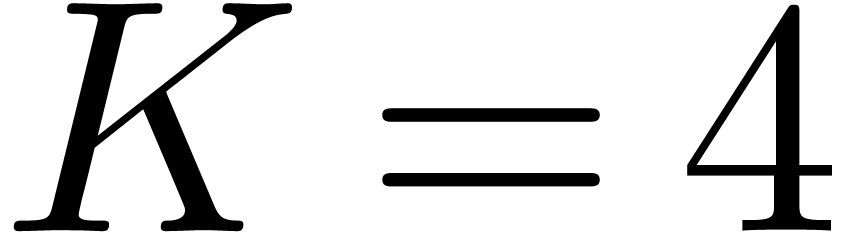 .
.