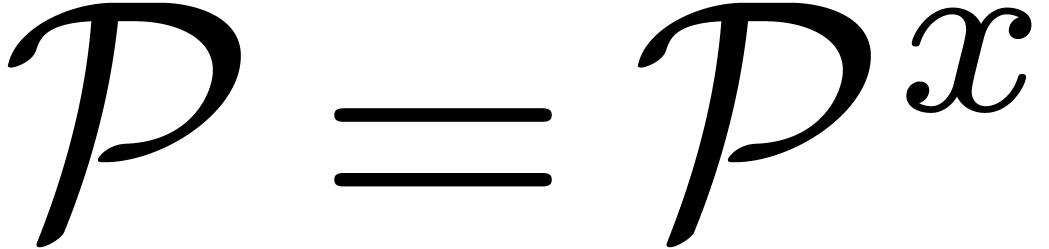 denote the ring of
analytic
denote the ring of
analytic 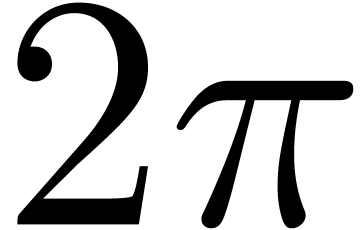 -periodic functions
in
-periodic functions
in 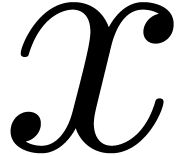 on the real axis. Let
on the real axis. Let
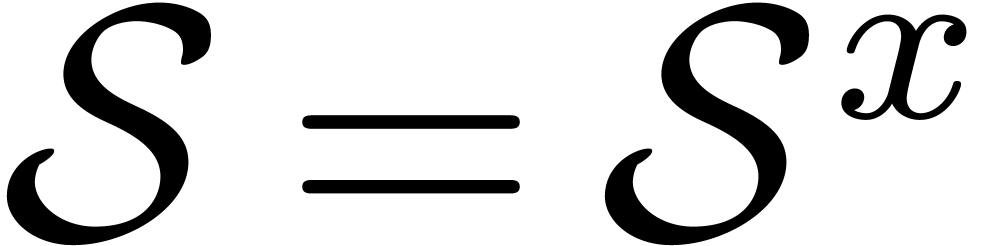 denote the ring of formal
Laurent series in
denote the ring of formal
Laurent series in 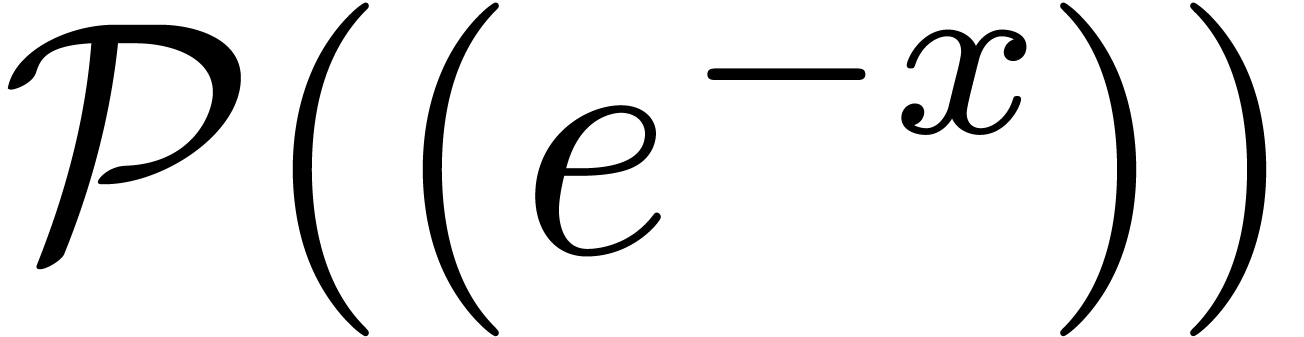 , whose
coefficients are defined on a common strip neighbourhood of the
real axis. In this paper, we study the linear differential equation
, whose
coefficients are defined on a common strip neighbourhood of the
real axis. In this paper, we study the linear differential equation
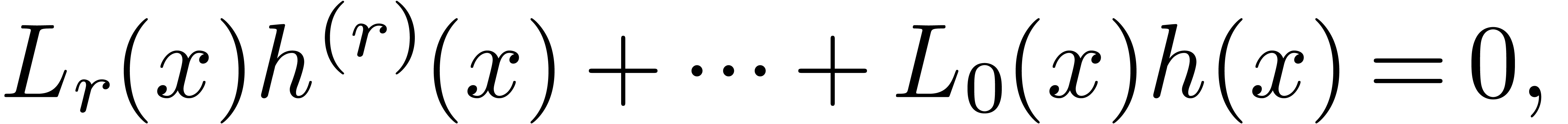
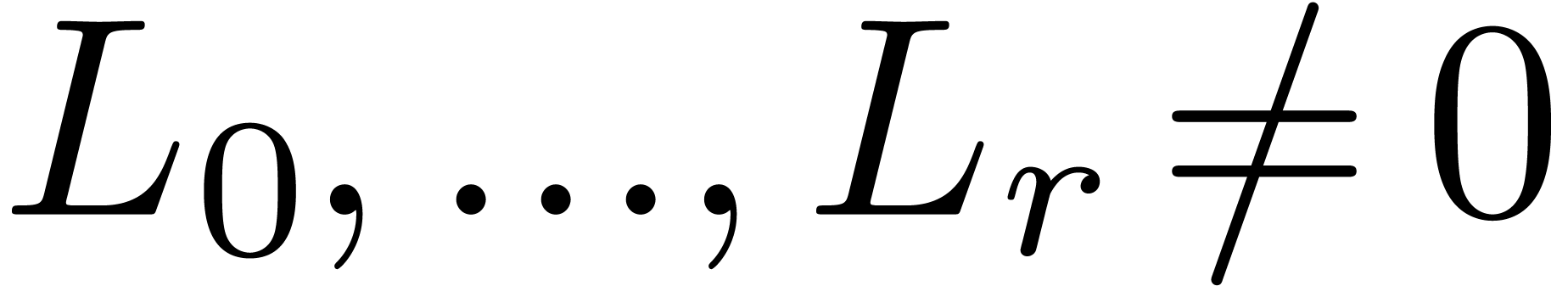 in
in  . We prove that, after a change of
variables
. We prove that, after a change of
variables 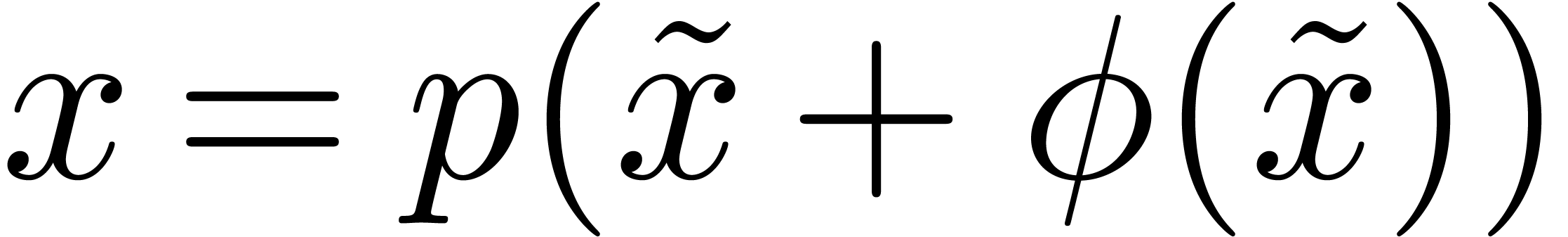 with
with 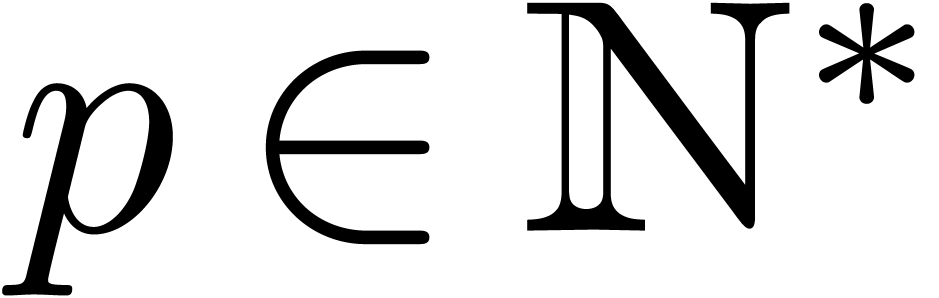 and
and 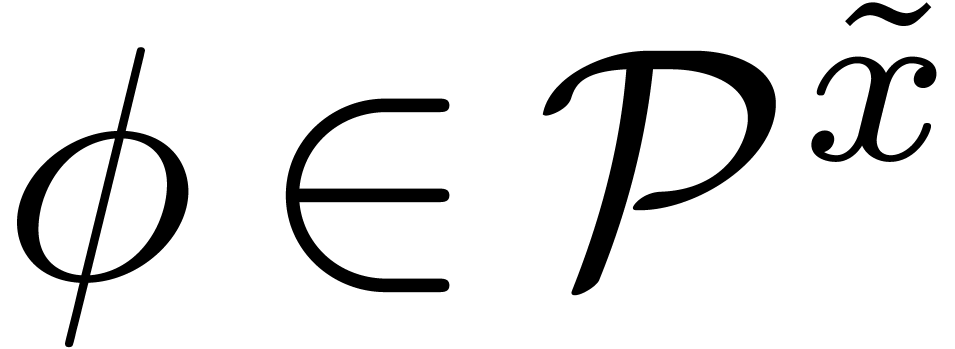 ,
this equation admits a basis of
,
this equation admits a basis of 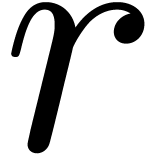 formal solutions of the form
formal solutions of the form
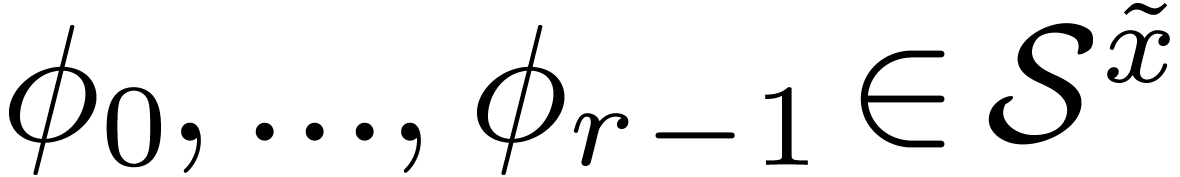 ,
, 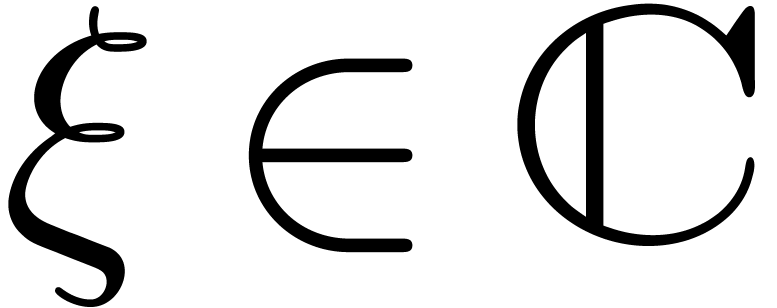 and
and 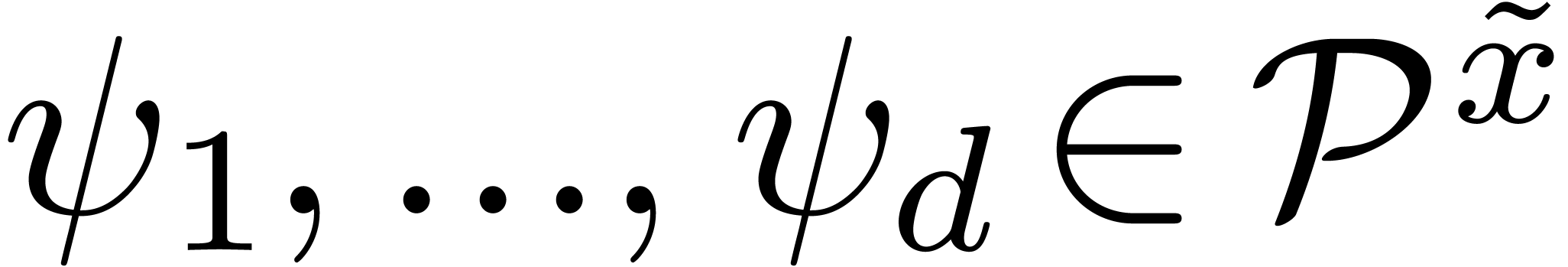 .
This generalizes a well known result when
.
This generalizes a well known result when  is replaced by
is replaced by  .
.