Abstract
A transseries is a generalization of a formal power series, constructed
from the real numbers and an indeterminate 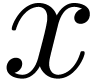 ,
using exponentiation, logarithm and infinite summation. Transseries may
be used to model the asymptotic behaviour of non-oscillating solutions
to non-linear differential equations and more general functional
equations. They form a totally ordered field, which is closed under
differentiation, integration, functional composition and inversion, as
well as the resolution of algebraic differential equations of odd
degree.
,
using exponentiation, logarithm and infinite summation. Transseries may
be used to model the asymptotic behaviour of non-oscillating solutions
to non-linear differential equations and more general functional
equations. They form a totally ordered field, which is closed under
differentiation, integration, functional composition and inversion, as
well as the resolution of algebraic differential equations of odd
degree.
The theory of transseries finds its origins in at least three different
areas of mathematics: analysis, model theory and computer algebra. In
analysis, they play a crucial role in Écalle's proof of Dulac's
conjecture, which is closely related to Hilbert's 16-th problem. From a
model-theoretic point of view, the field of transseries forms a model
for many interesting theories, which mix differentiation and other
operations, like an ordering or a valuation. Finally, transseries admit
a very constructive calculus, which makes them particularly suitable as
a framework for automatic asymptotics.
The aim of the present book is to provide a self-contained introduction
to the theory of transseries. The book focuses on that part of the
theory which should be of common interest for mathematicians working in
analysis, model theory or computer algebra, but many exercises have been
included for further studies. We hope that it will be suitable for both
graduate students and professional mathematicians.
View: Buy, Html, TeXmacs,
Pdf, BibTeX
Corrected version: Pdf, Errata
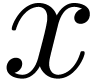 ,
using exponentiation, logarithm and infinite summation. Transseries may
be used to model the asymptotic behaviour of non-oscillating solutions
to non-linear differential equations and more general functional
equations. They form a totally ordered field, which is closed under
differentiation, integration, functional composition and inversion, as
well as the resolution of algebraic differential equations of odd
degree.
,
using exponentiation, logarithm and infinite summation. Transseries may
be used to model the asymptotic behaviour of non-oscillating solutions
to non-linear differential equations and more general functional
equations. They form a totally ordered field, which is closed under
differentiation, integration, functional composition and inversion, as
well as the resolution of algebraic differential equations of odd
degree.