Abstract
Let 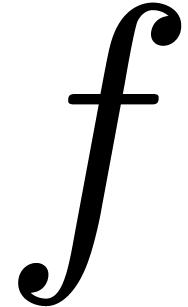 and
and  be two convergent power series in
be two convergent power series in 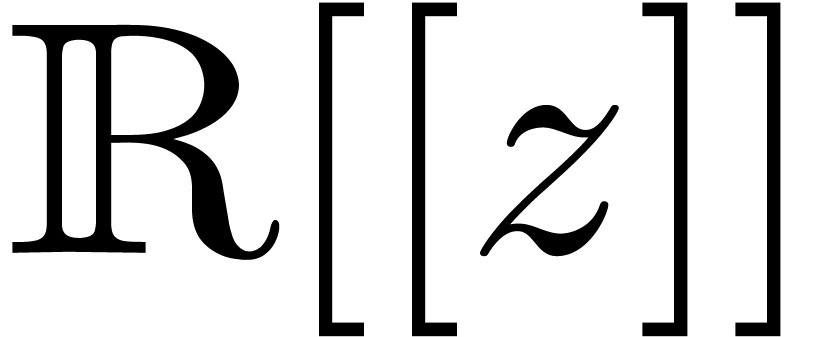 or
or 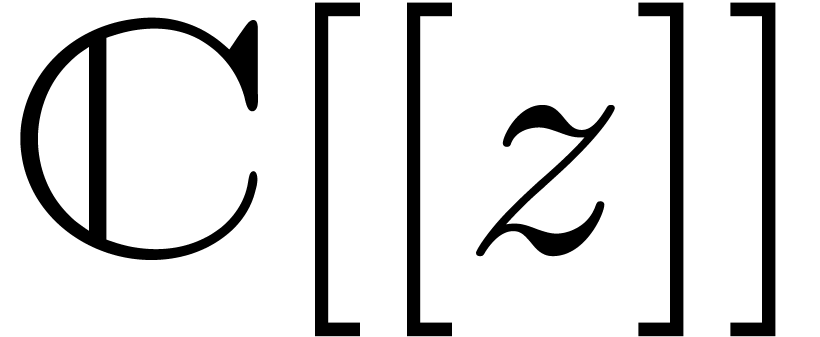 ,
whose first
,
whose first 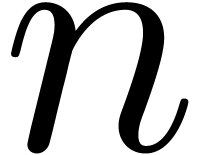 terms are given
numerically with a
terms are given
numerically with a 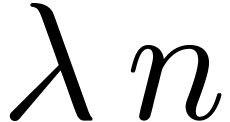 -bit
precision for a fixed constant
-bit
precision for a fixed constant  .
Assuming that
.
Assuming that 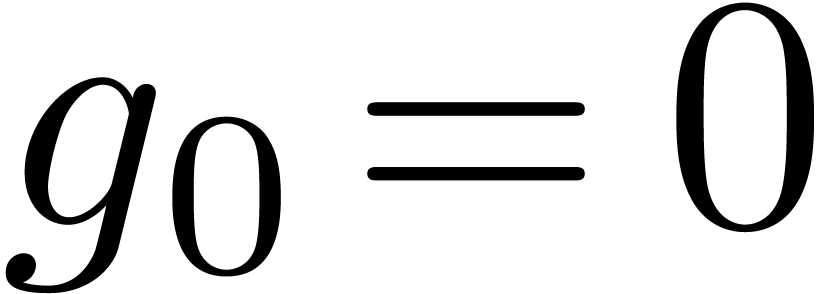 , we will show
in this paper that the first
, we will show
in this paper that the first 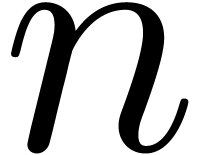 coefficients of
coefficients of  can be
computed with a
can be
computed with a 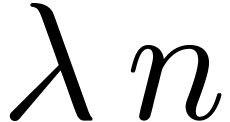 -bit
precision in time
-bit
precision in time 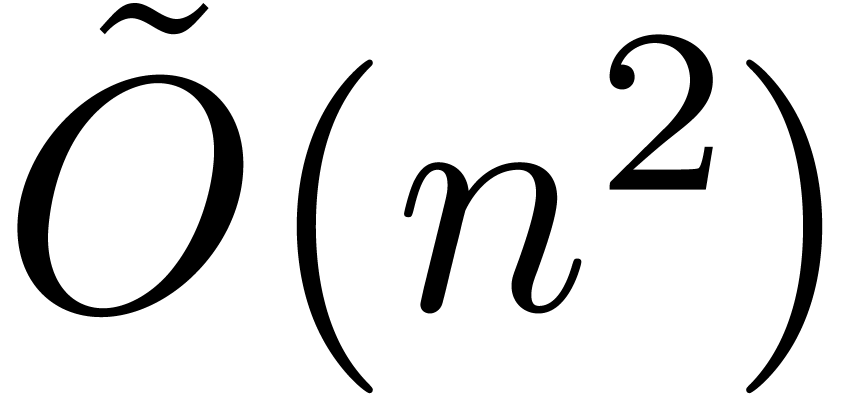 . Using
Newton iteration, a similar complexity bound holds for power series
reversion of
. Using
Newton iteration, a similar complexity bound holds for power series
reversion of  . Our method
relies on fast multi-point evaluation, which will be recalled and
further detailed for numeric polynomials. We also discuss relaxed
variants of our algorithm.
. Our method
relies on fast multi-point evaluation, which will be recalled and
further detailed for numeric polynomials. We also discuss relaxed
variants of our algorithm.
Keywords: power series, composition, FFT, multi-point
evaluation, algorithm
A.M.S. subject classification: 40-04, 42-04, 68W40
View: Html, TeXmacs, Pdf,
BibTeX
Remark. The anonymous referees pointed me to [1], which
contains many of the results presented in this paper. Nevertheless, some
details in the presentation may still be of interest, such as the
results in section 3.2. Also, we discuss relaxed variants of the main
composition algorithm.
[1] P Ritzmann. A fast numerical algorithm for the composition of power
series with complex coefficients. TCS, 44(1):1–16, 1986.
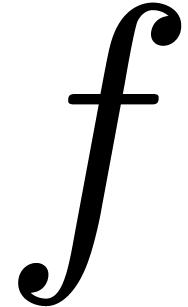 and
and  be two convergent power series in
be two convergent power series in 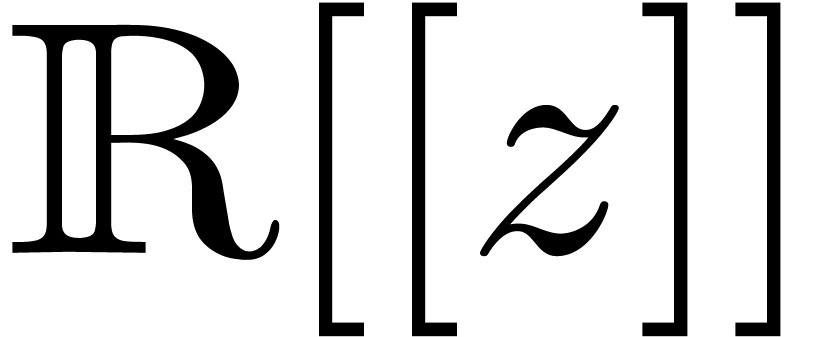 or
or 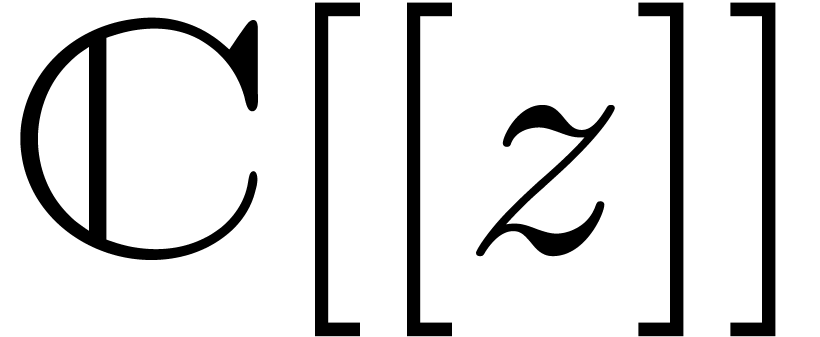 ,
whose first
,
whose first 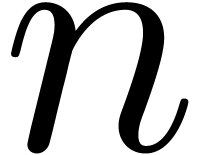 terms are given
numerically with a
terms are given
numerically with a 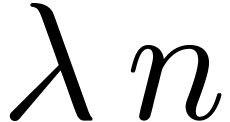 -bit
precision for a fixed constant
-bit
precision for a fixed constant  .
Assuming that
.
Assuming that 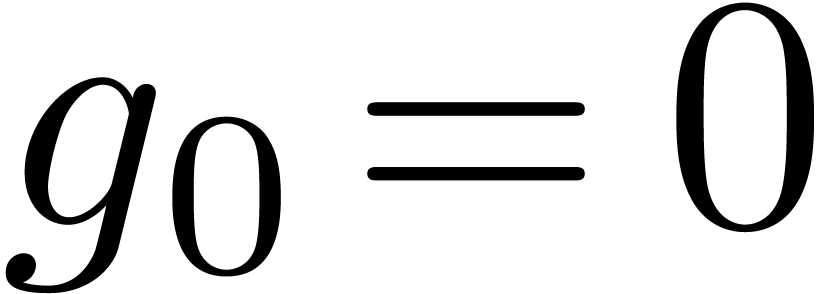 , we will show
in this paper that the first
, we will show
in this paper that the first 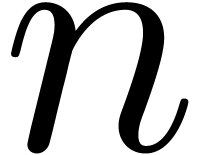 coefficients of
coefficients of  can be
computed with a
can be
computed with a 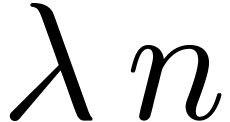 -bit
precision in time
-bit
precision in time 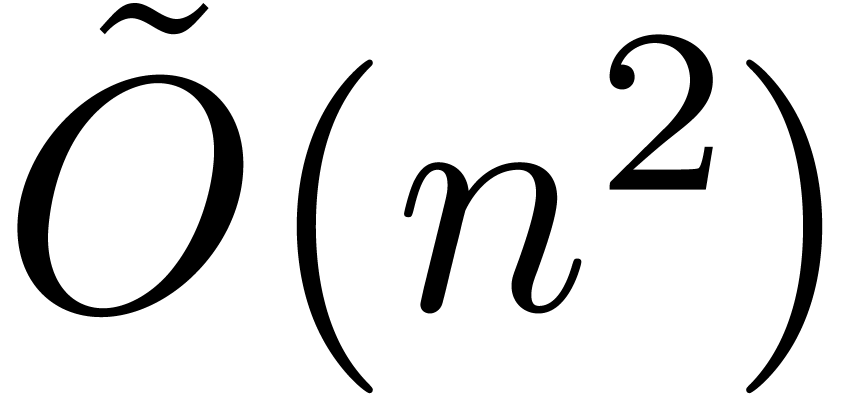 . Using
Newton iteration, a similar complexity bound holds for power series
reversion of
. Using
Newton iteration, a similar complexity bound holds for power series
reversion of  . Our method
relies on fast multi-point evaluation, which will be recalled and
further detailed for numeric polynomials. We also discuss relaxed
variants of our algorithm.
. Our method
relies on fast multi-point evaluation, which will be recalled and
further detailed for numeric polynomials. We also discuss relaxed
variants of our algorithm.