Abstract
Assuming a widely-believed hypothesis concerning the least prime in an
arithmetic progression, we show that two 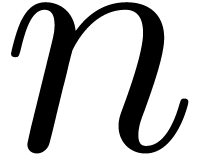 -bit
integers can be multiplied in time
-bit
integers can be multiplied in time 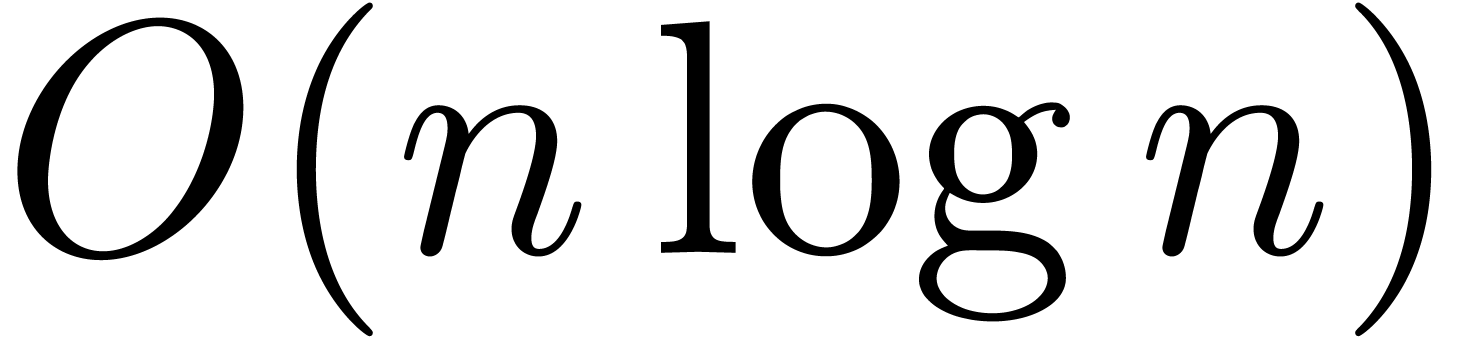 on a Turing machine with a finite number of tapes; we also show that
polynomials of degree less than
on a Turing machine with a finite number of tapes; we also show that
polynomials of degree less than 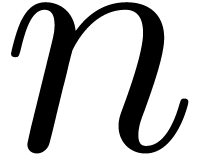 over a finite field
over a finite field 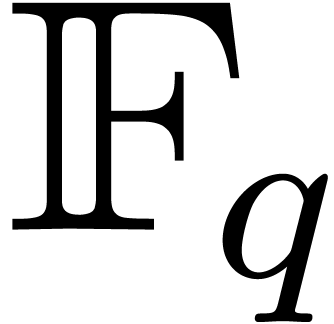 with
with
 elements can be multiplied
in time
elements can be multiplied
in time 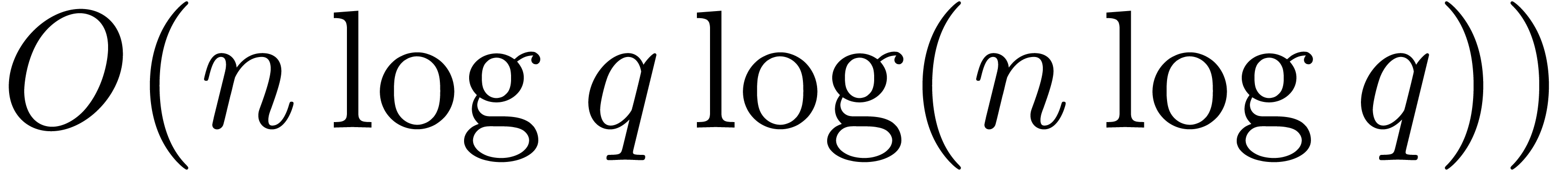 , uniformly in
, uniformly in  .
.
Authors: David Harvey, Joris van der Hoeven
Keywords: polynomial multiplication, integer
multiplication, algorithm, complexity bound, FFT, finite field
View: Html, TeXmacs, Pdf,
BibTeX
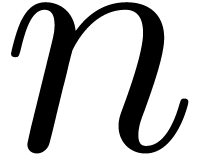 -bit
integers can be multiplied in time
-bit
integers can be multiplied in time 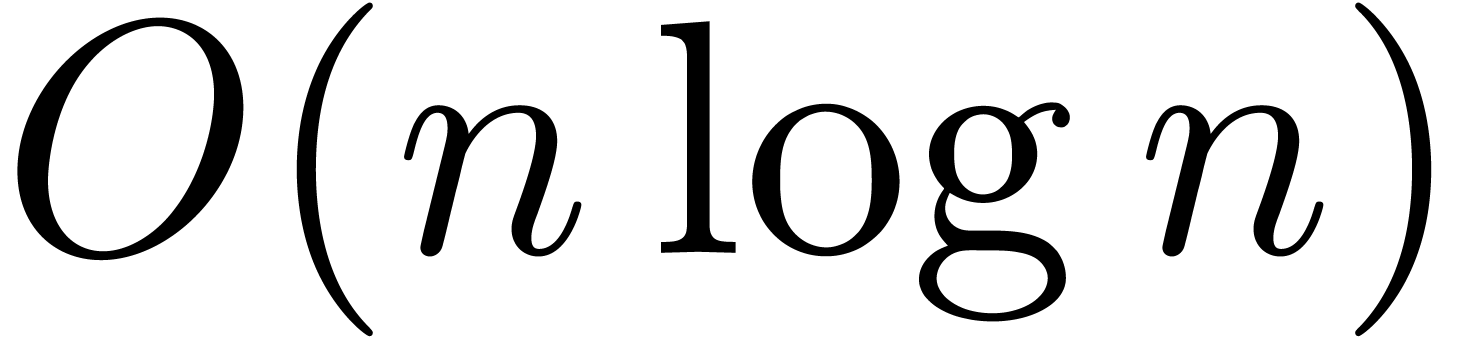 on a Turing machine with a finite number of tapes; we also show that
polynomials of degree less than
on a Turing machine with a finite number of tapes; we also show that
polynomials of degree less than 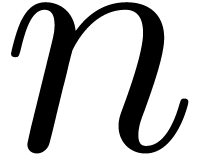 over a finite field
over a finite field 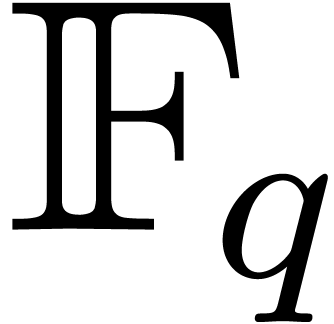 with
with
 elements can be multiplied
in time
elements can be multiplied
in time 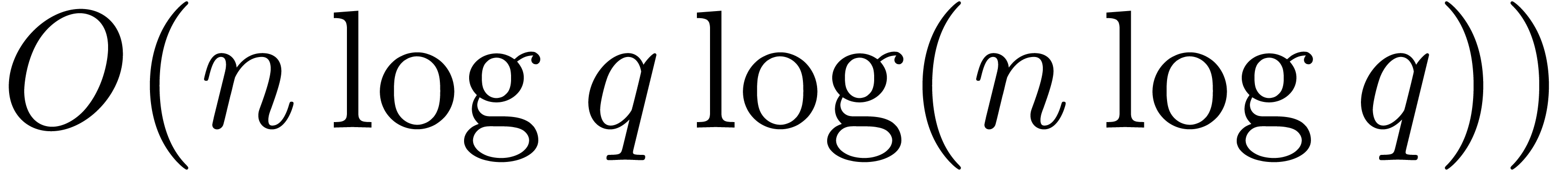 , uniformly in
, uniformly in  .
.