Abstract
Let 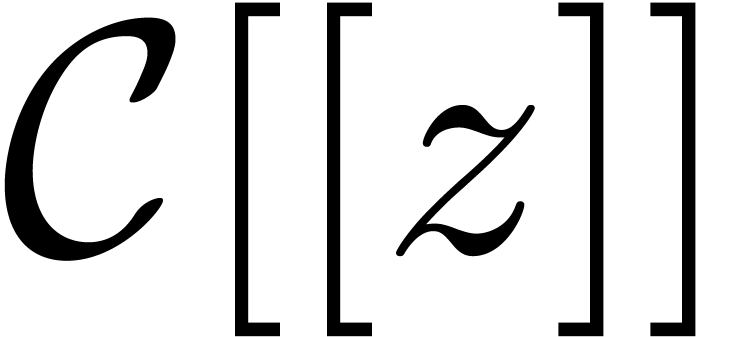 be the ring of power
series over an effective ring
be the ring of power
series over an effective ring 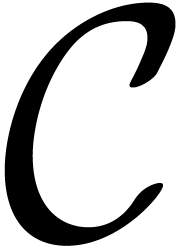 .
Brent has first shown that differential equations over
.
Brent has first shown that differential equations over  may be solved in an asymptotically efficient
way using Newton's method. More precisely, if
may be solved in an asymptotically efficient
way using Newton's method. More precisely, if 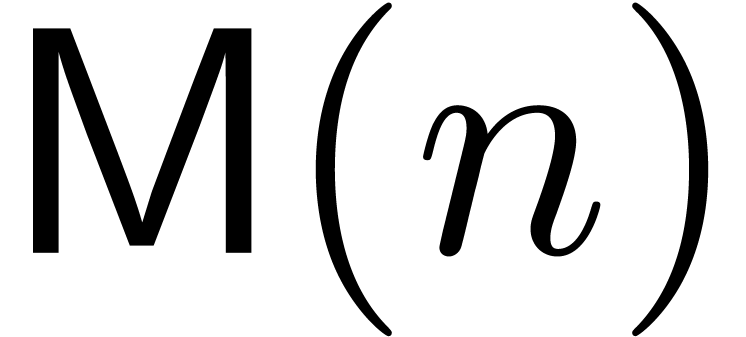 denotes the complexity in order two polynomials of
degree
denotes the complexity in order two polynomials of
degree 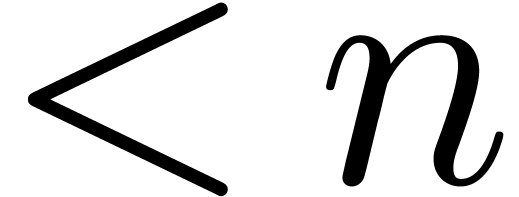 over
over 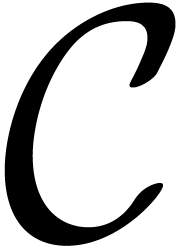 , then the first
, then the first 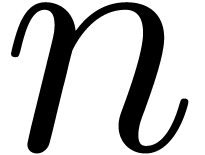 coefficients of the solution can be computed in time
coefficients of the solution can be computed in time 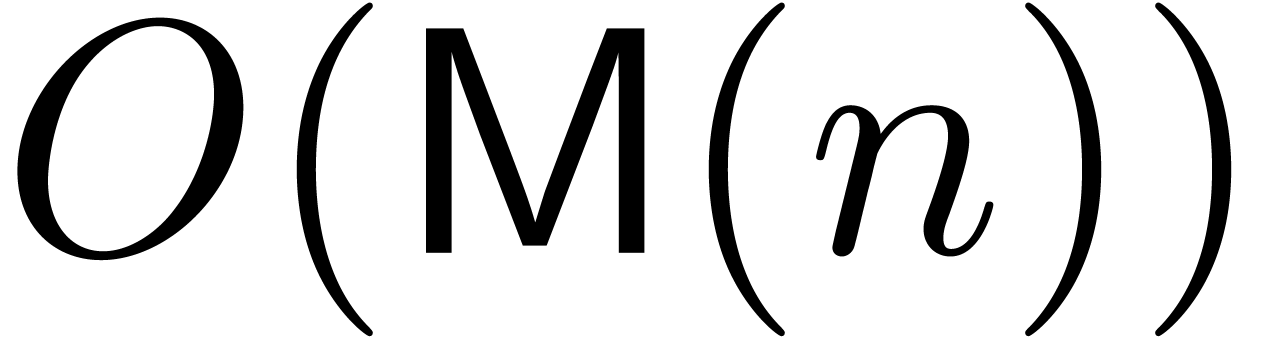 . However, this complexity does not take into
account the dependency of on the order
. However, this complexity does not take into
account the dependency of on the order 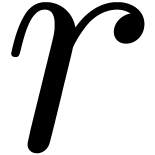 of the equation, which is exponential for the original method and linear
for a recent improvement. In this paper, we present a technique to get
rid of this constant factor, by applying Newton's method up to an order
like
of the equation, which is exponential for the original method and linear
for a recent improvement. In this paper, we present a technique to get
rid of this constant factor, by applying Newton's method up to an order
like 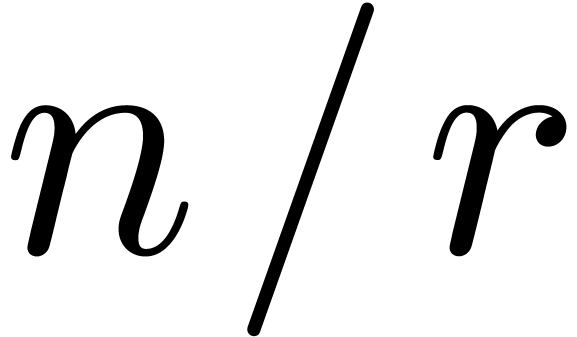 and trading the
remaining Newton steps against a lazy or relaxed algorithm in a suitable
FFT model.
and trading the
remaining Newton steps against a lazy or relaxed algorithm in a suitable
FFT model.
Keywords: power series, Newton's method, differential
equation, FFT
A.M.S. subject classification: 68W25, 37M99, 90C53,
42-04, 68W30, 33F05
View: Html, TeXmacs, Pdf,
BibTeX
Revisited Version: Html, TeXmacs,
Pdf, BibTeX
 be the ring of power
series over an effective ring
be the ring of power
series over an effective ring 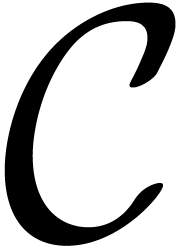 .
Brent has first shown that differential equations over
.
Brent has first shown that differential equations over  may be solved in an asymptotically efficient
way using Newton's method. More precisely, if
may be solved in an asymptotically efficient
way using Newton's method. More precisely, if 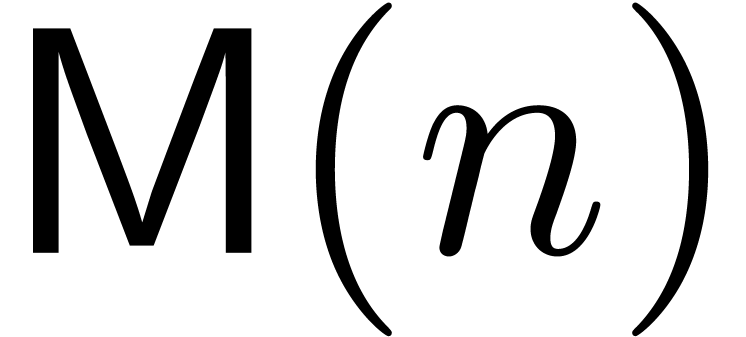 denotes the complexity in order two polynomials of
degree
denotes the complexity in order two polynomials of
degree 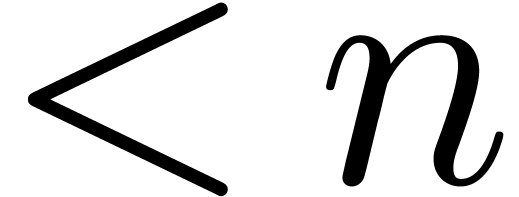 over
over 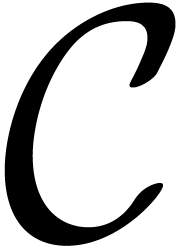 , then the first
, then the first 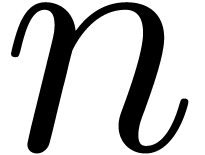 coefficients of the solution can be computed in time
coefficients of the solution can be computed in time 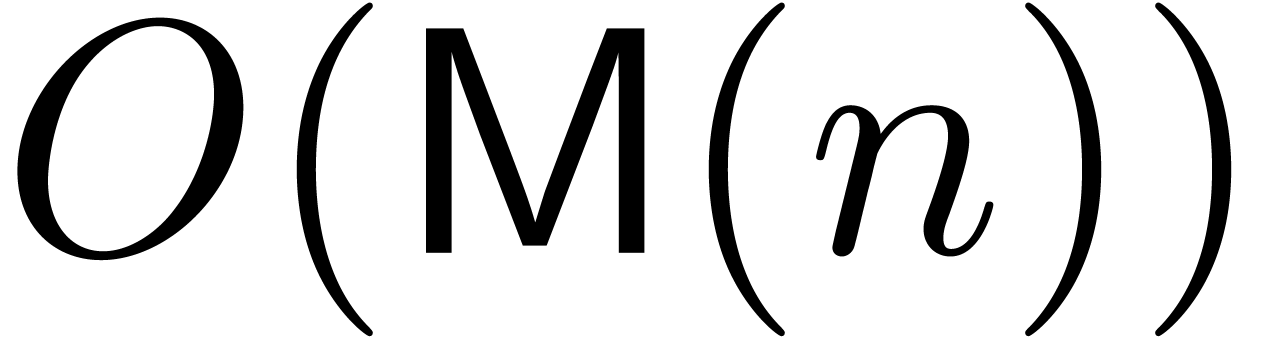 . However, this complexity does not take into
account the dependency of on the order
. However, this complexity does not take into
account the dependency of on the order 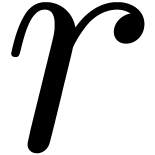 of the equation, which is exponential for the original method and linear
for a recent improvement. In this paper, we present a technique to get
rid of this constant factor, by applying Newton's method up to an order
like
of the equation, which is exponential for the original method and linear
for a recent improvement. In this paper, we present a technique to get
rid of this constant factor, by applying Newton's method up to an order
like 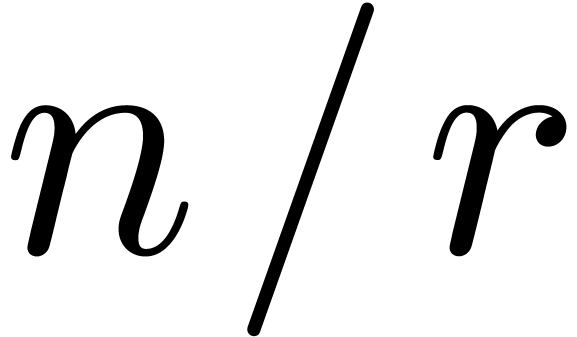 and trading the
remaining Newton steps against a lazy or relaxed algorithm in a suitable
FFT model.
and trading the
remaining Newton steps against a lazy or relaxed algorithm in a suitable
FFT model.