Abstract
How to automatically determine reliable error bounds for a numerical
computation? One traditional approach is to systematically replace
floating point approximations by intervals or balls that are guaranteed
to contain the exact numbers one is interested in. However, operations
on intervals or balls are more expensive than operations on floating
point numbers, so this approach involves a non-trivial overhead.
In this paper, we present several approaches to remove this overhead,
under the assumption that the function 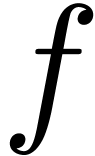 that we wish to evaluate is given as a straight-line program (SLP). We
will first study the case when the arguments of our function lie in
fixed balls. For polynomial SLPs, we next consider the
“global” case where this restriction on the arguments is
removed. We will also investigate the computation of bounds for first
and higher order derivatives of
that we wish to evaluate is given as a straight-line program (SLP). We
will first study the case when the arguments of our function lie in
fixed balls. For polynomial SLPs, we next consider the
“global” case where this restriction on the arguments is
removed. We will also investigate the computation of bounds for first
and higher order derivatives of 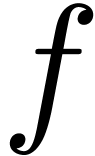 .
.
Authors: Joris van der Hoeven,
Grégoire Lecerf, Arnaud
Minondo
View: Html, TeXmacs, Pdf,
BibTeX
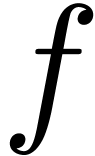 that we wish to evaluate is given as a straight-line program (SLP). We
will first study the case when the arguments of our function lie in
fixed balls. For polynomial SLPs, we next consider the
“global” case where this restriction on the arguments is
removed. We will also investigate the computation of bounds for first
and higher order derivatives of
that we wish to evaluate is given as a straight-line program (SLP). We
will first study the case when the arguments of our function lie in
fixed balls. For polynomial SLPs, we next consider the
“global” case where this restriction on the arguments is
removed. We will also investigate the computation of bounds for first
and higher order derivatives of 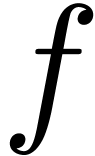 .
.