Abstract
Consider two polynomials 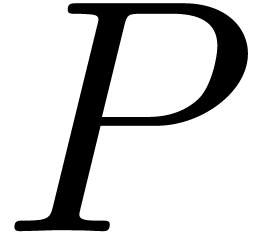 and
and
 with multiple precision
floating point coefficients. Although the product
with multiple precision
floating point coefficients. Although the product 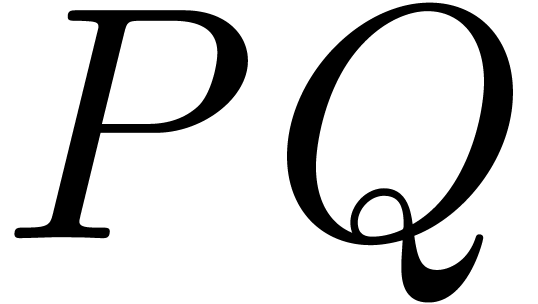 can in principle be computed efficiently using FFT
multiplication, this algorithm is numerically stable only if the
coefficients of
can in principle be computed efficiently using FFT
multiplication, this algorithm is numerically stable only if the
coefficients of 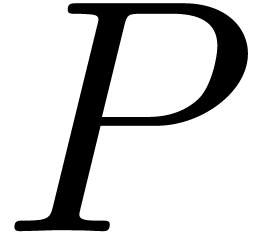 are of the
same order of magnitude and similarly for
are of the
same order of magnitude and similarly for  .
In this paper, we present a new asymptotically fast multiplication
algorithm which has a “better” numerically stability. We
also provide some theoretical support for what we feel to be
“better”, by introducing the concept of “relative
Newton error”.
.
In this paper, we present a new asymptotically fast multiplication
algorithm which has a “better” numerically stability. We
also provide some theoretical support for what we feel to be
“better”, by introducing the concept of “relative
Newton error”.
Keywords: polynomial, floating point number,
multiplication, algorithm, FFT
A.M.S. subject classification: 65T50, 42-04, 68W30
View: Html, TeXmacs, Pdf,
BibTeX
Errata. Unfortunately, an annoying error slipped into
the preprint: the bound (3) is wrong. Consequently, the complexity
estimates in the paper only work in one direction. Nevertheless, we have
implemented a first version of the algorithm in Mathemagix
and the approach works well in practice. In particular, we use it in the
implementation of a method for computing the roots of complex
polynomials using iterated Graeffe transforms and tangent numbers. We
observed a good asymptotic complexity for this root finder, although the
constant factor turned out to be rather bad.
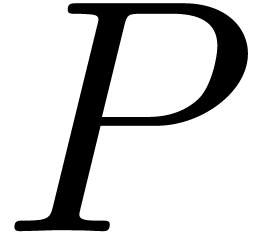 and
and
 with multiple precision
floating point coefficients. Although the product
with multiple precision
floating point coefficients. Although the product 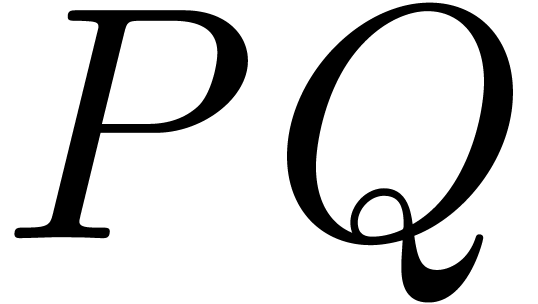 can in principle be computed efficiently using FFT
multiplication, this algorithm is numerically stable only if the
coefficients of
can in principle be computed efficiently using FFT
multiplication, this algorithm is numerically stable only if the
coefficients of 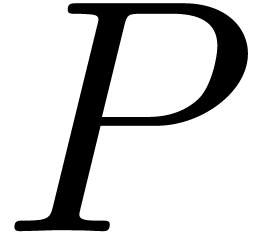 are of the
same order of magnitude and similarly for
are of the
same order of magnitude and similarly for  .
In this paper, we present a new asymptotically fast multiplication
algorithm which has a “better” numerically stability. We
also provide some theoretical support for what we feel to be
“better”, by introducing the concept of “relative
Newton error”.
.
In this paper, we present a new asymptotically fast multiplication
algorithm which has a “better” numerically stability. We
also provide some theoretical support for what we feel to be
“better”, by introducing the concept of “relative
Newton error”.