Computer algebra systems and TeXmacs

1.Axiom

Axiom is a general purpose Computer Algebra system. It is useful for research and development of mathematical algorithms. It defines a strongly typed, mathematically correct type hierarchy. It has a programming language and a built-in compiler.

Axiom has been in development since 1973 and was sold as a commercial product. It has been released as free software (under a BSD-like license).

Efforts are underway to extend this software to

• Develop a better user interface;

• Make it useful as a teaching tool;

• Develop an algebra server protocol;

• Integrate additional mathematics;

• Rebuild the algebra in a literate programming style;

• Integrate logic programming;

• Develop an Axiom Journal with refereed submissions.

Axiom web page : http://www.nongnu.org/axiom/

Axiom project : http://savannah.nongnu.org/projects/axiom

2.Giac

Giac Is A Computer algebra system. The system has been designed by Bernard Parisse and is under active development. It is a general-purpose computation kernel written in C++ with the following features.

Algebra

Arbitrary precision integers, integer and polynomial arithmetic, Gröbner bases, simplification, equation solver, partial fraction decomposition, linear algebra (vectors, matrices, row reduction to echelon form, eigenvalues and eigenvectors), permutations, combinatorial analysis, computing in 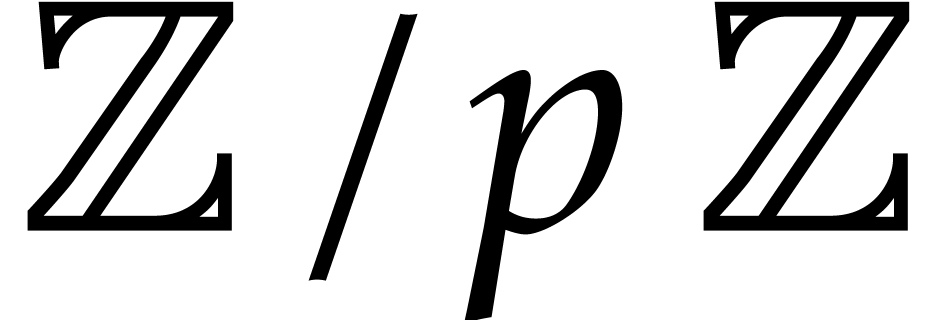and

Calculus

Derivatives, integration, limits, series expansion, vector calculus, calculus of variations, implicit differentiation, curve interpolation, differential equations, special functions

2D and 3D plotting

Function graphs, surfaces, plotting implicit curves, plotting the solution of a system of inequalities, polar and parametric plots, scatter and line plots, bar plots, pie charts, histograms

2D and 3D geometry

Points, segments, lines, triangles, polygons, circles, conics, parametric curves, curve intersection, tangents, planes, surfaces

Probability and statistics

Probability distributions, random variables, efficient sampling, maximum-likelihood fitting, statistical tests, kernel density estimation

Signal processing and audio tools

Convolution, (auto)correlation, continuous/fast Fourier transform, Fourier series, filtering, windowing, loading, creating and saving audio clips, audio playback, resampling, noise removal, waveform plotting, spectrum plotting

Optimization

Mixed integer linear programming, finding local and global extrema, nonlinear programming, transportation problem

Graph theory

Creating (random) graphs and digraphs, operations on graphs, modifying graphs, importing and exporting graphs to dot file format, examining properties of graphs, traversing graphs, vertex and edge coloring, graph isomorphism, graph drawing

Programming

Functions, local variables, conditionals, loops, choice of syntax (C-like, Python, Maple, Mupad, TI89)

Syntax compatibility with other systems

Maple compatibility, MuPAD compatibility, Python compatibility, MathML export (content and presentation), LaTeX export

Giac output is rendered in TeXmacs from its Scheme tree representation, which results in semantically correct formulas which can be copied back to Giac. Interactive plotting and mathematical input are supported as well.

A note on session plots.

3.GTybalt

GTybalt is a free computer algebra system which is built on top of GiNaC, CLN and a program to interpret C and C++ commands. gTybalt, which is still in an experimental stage, is maintained by Stefan Weinzierl. Some of the main features of gTybalt are the following:

• Object Oriented: gTybalt allows symbolic calculations within the C++ programming language.

• Efficiency for large scale problems: Solutions developed with gTybalt can be compiled with a C++ compiler and executed independently of gTybalt.

• Short development cycle: gTybalt can interpret C++ and execute C++ scripts. Solutions can be developed quickly for small-scale problems, either interactively or through scripts, and once debugged, the solutions can be compiled and scaled up to large-scale problems.

4.Macaulay 2

Macaulay2 is a new software system devoted to supporting research in algebraic geometry and commutative algebra. The software is available now in source code for porting, and in compiled form for Linux, SunOS, Solaris, Windows, and a few other Unix machines. An interface with TeXmacs is currently being implemented.

5.Maxima

Maxima is not only one of the oldest and best computer algebra systems around, it is also one of the only general purpose systems for which there is a free implementation. The current free Maxima implementation was started by William F. Schelter. It is dedicated to his memory. Here follow some features of Maxima:

• Plotting via netmath over the network.

• Computations over network

• Well tested on a large array of problems.

• Source level Debugger for maxima code

• Documentation available as html, texinfo, info, dvi and postscript. The documentation can be read inside TeXmacs.

• Easy to extend in fundamentally new ways, because you have complete access to source, and access to Common Lisp.

• Portable to many systems.

6.Pari

Pari-gp is a software package for computer-aided number theory. It consists of a C library, libpari (with optional assembler cores for some popular architectures), and of the programmable interactive gp calculator. While you can write your own libpari-based programs, many people just start up a gp session, or have gp execute their scripts. Pari sessions can now be started inside TeXmacs.

Developed at Bordeaux by a team led by Henri Cohen, PARI-GP is now maintained by Karim Belabas with the help of many volunteer contributors.

7.Reduce

Reduce is one of the oldest computer algebra systems. It is powerful, stable and highly efficient. Its TeXmacs interface is described in the arXiv article.

8.Sage

Sage is an open source system for mathematical computations. It is written in Python and provides interfaces for a wide variety of other systems, such as Axiom, Gap, Pari GP, Macaulay2, Maxima, Octave, and Singular. The system was started by William Stein.

9.Yacas

Yacas is, as it's name suggest, yet another computer algebra system. Things implemented include: arbitrary precision, rational numeric, vector, complex, and matrix computations (including inverses and determinants and solving matrix equations), derivatives, solving, Taylor series, numerical solving (Newtons method), and a lot more non-mathematical algorithms. The language natively supports variables and user-defined functions. There is basic support for univariate polynomials, integrating functions and tensor calculations. Yacas is still under development.