 )
or indirectly (like
)
or indirectly (like 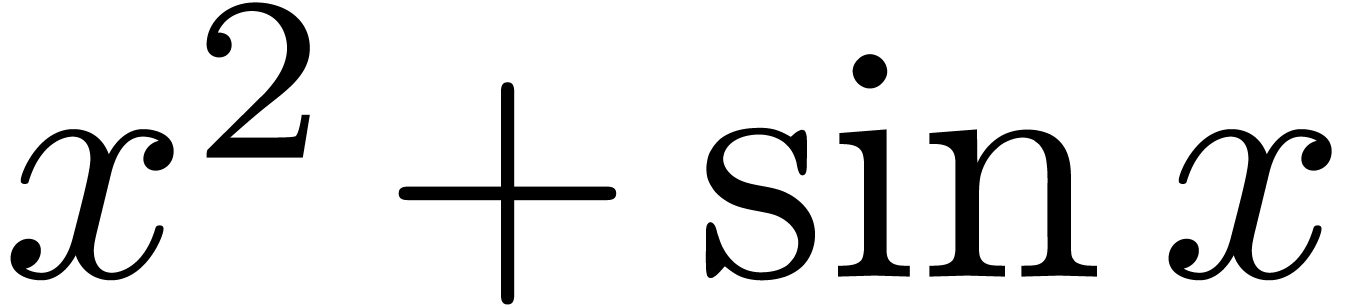 ).
).
| HomepagePublicationsTalksTeXmacsMathemagix |
Consider an algebraic differential equation with real coefficients. A
solution at infinity is said to be tame, if it does not involve any
oscillation, either directly (like  )
or indirectly (like
)
or indirectly (like 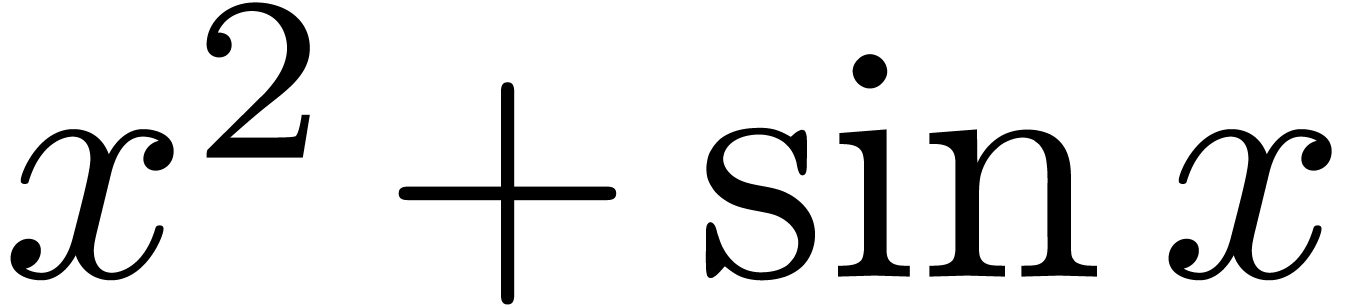 ).
).
The subject of asymptotic differential algebra studies such solutions from a formal standpoint. This can be done in the language of differential algebra enriched with an ordering or a valuation. Imposing a few natural compatibility axioms between the derivation and the ordering leads to the theory of H-fields.
Three important examples of H-fields are Hardy fields, transseries, and
the surreal numbers. Hardy fields are differential fields of germs of
real functions at infinity. Transseries are formal expressions that can
be obtained from real numbers and an infinitely large variable 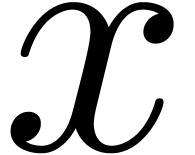 , using exponentiation, logarithms,
and infinite summation. Surreal numbers were introduced by Conway and
Berarducci and Mantova recently constructed a derivation on the field of
surreal numbers.
, using exponentiation, logarithms,
and infinite summation. Surreal numbers were introduced by Conway and
Berarducci and Mantova recently constructed a derivation on the field of
surreal numbers.
Transseries satisfy several strong closure properties: they are closed under solving linear first order equations and they satisfy a differential intermediate value property. These properties are captured through the notion of H-closed H-fields. The theory of H-closed H-fields is model complete and is the model companion of the theory of H-fields.
The surreal numbers with Berarducci-Mantova's derivation is another examples of an H-closed H-field. Recently, we showed that all so-called maximal Hardy fields are also H-closed.
In our course, we will give an introduction to transseries, Hardy fields, the theory of asymptotic differential algebra, and the model theory of H-fields. The aim is to provide a good entry point for the more voluminous books that Matthias Aschenbrenner, Lou van den Dries, and I wrote on this topic.
Occasion: IMS Graduate Summer School in Logic, Singapore, July 10–14, 2023
Documents:
Lesson 1: Hausdorff fields
Lesson 2: Hardy fields
Lesson 3: Generalized power series
Lesson 4: Newton polygon method
Lesson 5: Transseries
Lesson 6: Linear differential equations over 
Lesson 7: Algebraic differential equations over 
Lesson 8: Valued fields
Lesson 9: H-fields
Lesson 10: H-closed H-fields